Generating Fractals with Recursion

Find all code, pictures, and documentation for the article at github.com/robotgyal/generating-fractals-with-recursion.

In order fo you to have made it here, you either have an interest in recursion, fractals, or cool images made with code. I aim to have you interested in all of the above by the end of our journey.

Let us begin at the beginning,

What is recursion?

A simple explanation for recursion would be an operation that will call itself, upon itself. More precisely, Merriam Webster defines it as,

Both definitions identify the idea of a knowing and iteracting with a self.

A visual may provide more insight.

A quick google search of recursion will provide interesting and unexpected results.

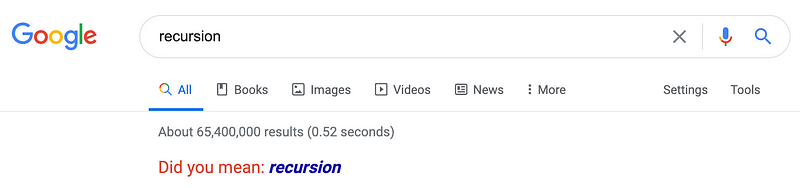
I clicked the recommended recursion suggestion (way too many times) to check for a change in result. To no avail. No matter how many times I clicked recursion, I was redirected back to the same page, suggesting the same thing over, and over, again.

This provides an excellent representation of our core topic: recursion. Defning something with itself.

As a mathematical and technical concept, it can begin to go to daunting but fascinating places such as chaos theory, abstract complexity theory, and inductive inference. However our main focus is on Fractals.

This begs the further question:

What are Fractals?

Aware of the definition or not, I can almost guarantee that you have seen one before in your lifetime. If not, let me provide some common and/or cool examples for you.

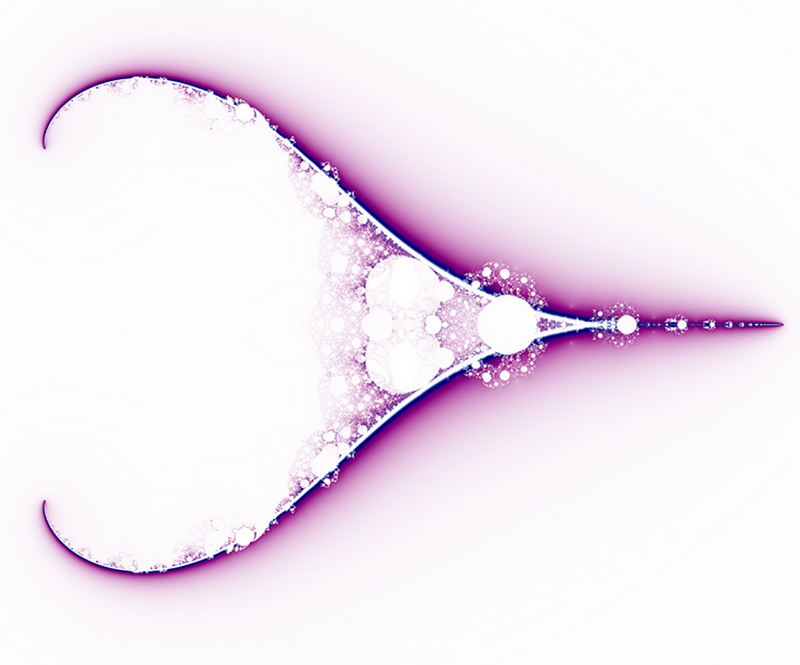
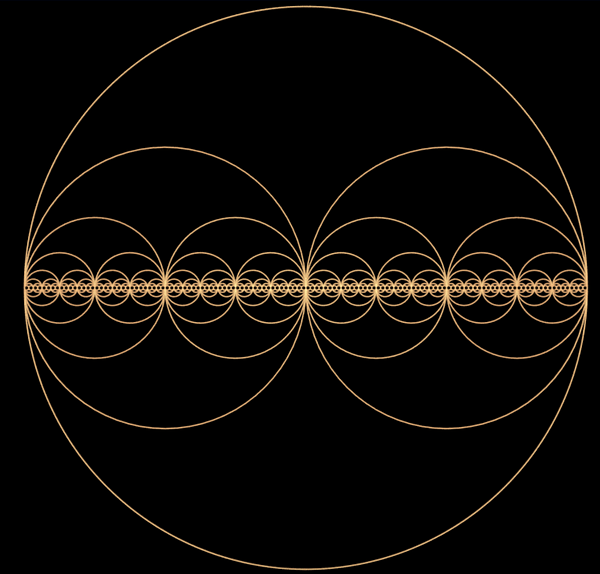
Binoculars 2. Circular Infinity 3. Reverse Julia 4. Fractal Space Filling — http://paulbourke.net/fractals/

Originating from the Latin word ‘fractus’, meaning “interrupted, irregular” -> literally ‘broken’, it is is not too much of a task to see why this name was chosen from looking at these images.

Coined by Mandelbrot in ‘Fractals’, it is also known by other names such as:

A self-similar shape

Pictures of Chaos

Neverending Patterns

But one of the most important elements of fractals is the idea of self-similarity. No matter how much you zoom in or out, or how long you perform either of those actions, the result will show the same types of patterns and structures as the original — only truly limited by the power of the computer it is running on.

More often than not, these fractal shapes are used to emulate and copy organic shapes in nature. Trees, mountians, clouds, snowflakes, waves, wings, etc.

Nature is not created in straight lines and so neither should our creations!

Let us create our own fractals!

We are going to use python3 and Processing.py to run our code.

If you are unfamiliar with getting started with Processing.py, please dowload Processing here.

Once installed, follow the instructions here to convert to Python mode.

Find out more about Getting Started with Processing,py here: Getting Started

Our first fractal is known as The Cantor Set. Simply stated, it illustrates starting with a line, breaking it in 2, then breaking each other into two, and so on and so forth indefinitely. (I know I said we don’t draw in straight lines but we have to start somewhere). Does this loop presented here, of doing the same action repeatedly on itself, sound familiar?

Recursion!

We are going to start by defining a function for this fractal.

def cantor(x, y, len):  
     pass

The x and y here represent the location of our lines. The len will be the length of our line.

Next we are going to setup a condition for the recursion

if len >=1:  
   line(x, y, x+len, y)  
          
   y+=20

As long as the length of our line is at least 1, we should draw a line that start at x,y and end at x+len, y. We then move down 20 increments to make space for the next set of lines.

Here is the interesting part. We want to use this ‘formula’ again on more and more lines, based on what happens with the current lines. We then call the funtion inside of itself.

cantor(x, y, len/3)  
cantor(x+len*2/3, y, len/3)

This allows for the next 2 lines to be drawn that are the split version of the lines before it. Let’s put it all together and look visually.

cantor.pyde gist

Observe how each level is has 2 further broken lines based on the number of previous lines. Not too bad, right? Let try another.

Let’s lean a bit more into natural systems and create a Recursive Fractal Tree.

We are going to start in a similar fashion as before with defining a function, and settting up our basic functionality. In this case we are creating branchs of a ceratin length, len, and will branch off at an angle, theta. Theta can be set to any value, and you can experiment to find what works best for you. We, however, are going to do a bit more tweaking so that the angle of our tree branches will be based off the horizontal location of our mouse.

def branch(len, theta):  
  line(0, 0, 0, -len);  
  translate(0, -len);  
   
  len *= 0.66;

translate() moves the current position on the screen and helps with visibility.

Next we create our branches. We repeat the main action twice, as we want 2 more branches per cycle.

pushMatrix() and popMatrix() are built in functions that help to preserve data, similar to stacks.

More on these here pushMatrix() / popMatrix()

if (len > 2):  
    pushMatrix()  
    rotate(theta)  
    branch(len, theta)  
    popMatrix()  
   
    pushMatrix()  
    rotate(-theta)  
    branch(len, theta)  
    popMatrix()

Let’s complete the code and view our image!

Pretty cool, right?

There are so many different ways to drastically alter this visual, from the color and size, to branch count, generated angles, and much, much more!

Finally, we are going to tackle one of the most famous and recognizable fractals: The Mandelbrot Set.

“The Mandelbrot set can be explained with the [quadratic recurrence] equation zn+1 = zn2 + c. In that equation, c and z are complex numbers and n is zero or a positive integer (natural number).”

This is a higher level fractal that, for deeper use, will require a good knowledge of high level math principles. For our purposes we are going to use the following to implement. For more in depth explanations visit:

The Mandelbrot Set by Daniel Shiffman

Mandelbrot Set — Wolfram Alpha

def setup():  
    global zmx1, zmx2, zmy1, zmy2  
    size(500, 500)  
    zmx1 = int(width / 4)  
    zmx2 = 2  
    zmy1 = int(height / 4)  
    zmy2 = 2  
   
def draw():  
    global i  
   
    if i <= width:  
        i += 1  
    x = float(i + di) / zmx1 - zmx2  
    for j in range(height + 1):  
        y = zmy2 - float(j + dj) / zmy1  
        a = b = aa = bb = 0  
        cr, ci = x, y  
        n = 1  
        while n < 200 and (aa + bb) < 4:  
            aa = a * a  
            bb = b * b  
            a = 2 * a * b + ci  
            b = bb - aa + cr  
            n += 1

That’s quite a lot but the results that we get are more than worth it. Let’s add some finishing touches to our code to add color, and the functionality to zoom into the fractal via mouseclick.

Here’s our results….

Upon clicking and zooming in (while running in Processing), we find even more interesting results.

The concept of self-similarity becomes apparant as we look at these images. It’s even more amazing to see the types of images we can get from just a handful of lines of code. It illustrates the power of recursion when used computationally.

But, I’m sure you’re wondering, if recursion can be used to create such images, what else can it be used for?

The most notable is Linked Lists and Search Algortihms, especially Binary Search →Searching a sorted list by repeatedly cutting the list in half. It often takes more memory and computation in comparison to doing it iteratively, but recursion is often simplier and, in more rare cases, the only option available due to programming language limitations.

It is also often used for solving games and puzzles, such as Sudoku and The Towers of Hanoi.

As you get deeper into Dynamic Programming and approach subjects such as Machine Learning, many possibilities become possible using recursion, such as, prediction, classification, pattern recognition, and model training.

As we wrap things us, we need to circle back to the beginning with our current information. Recursive summarizing.

Fractals are beautiful designs of nature built off the principles of chaos and mathematics. With the growth of computational processes over the years, we are able to code examples of these processes. One of the ways in which we achieve this is through recursion, which is a powerful concept for executing processes continuously.

“In order to understand recursion, one must understand recursion.” ~Stephen Hawking

As we move forward with advancements in programming, math, and science, I implore you to keep out for developments in this field.

I have attached a few more varieties of fractals I have built.

Perhaps even utilize these, and similar functions, to create your own customized versions.

“A fractal is a way of seeing infinity”

Benoit Mandelbrot

Barnsley Fern

Lorenz Attractor

REFERENCES