As you progress in your studies of Computer Science, you will come across the concept of Big O Notation. This concept is usually introduced right before learning concepts such as Data Structures and Algorithms.

Photo by Rocco Stoppoloni on Unsplash
Why?
Because, just like in life, there are often many solutions to solving a single problem and knowing the pros and cons of each is crucial to making a good decision.
While I won’t be covering the different algorithms that Big O pertains to, I will be giving a quick understanding of Big O so as to ease you into the more in depth concepts of performing time and space analysis.
Basic breakdown
What exactly is this Big O notation, you may ask?
According to MIT —
Big O notation (with a capital letter O, not a zero), also called Landau’s symbol, is a symbolism used in complexity theory, computer science, and mathematics to describe the asymptotic behavior of functions. Basically, it tells you how fast a function grows or declines
Simply stated, it is a standardized way of measuring how long it takes for an algorithm to run based on the size of its input.
In a ‘normal’ coding session, the focus is on solving a problem, completing a task, or finishing a product. As users and data increase, the solution can break or bottleneck. As input in a system increases, so does the time it takes to perform actions on it.
Take for example, looking for a video to watch online. If you only had 2 choices, it won’t take long to make a decision. If you had 1,000,000 videos, it takes more time to go through each to find a good one.
This is when it becomes crucial to focus on time complexity and different techniques that can be used to reduce the time. Big O Notation has become the standard when it comes to communicating these times.
Think of it as its own unit of measurement. Rather than looking at milliseconds(ms) or nanoseconds(ns), we look at input size (n).
What really makes Big O Notation stand out against other measurements, are it’s rules of usage. These few rules make it more standardized, readable, transferable, and overall simplified.
Rules
- Ignore less significant figures
- As we scale upwards, the lesser order terms don’t have as significant an effect on the overall time calculations.
- Example: If our formula was set as f(x) = n² + n + 1, we only should consider the highest order term, in this case n². So if our n=10, we would get f(x) = 100 + 10 + 1. But if our n=100, we get 10,000 + 100 + 1. And as n continues to increase, the highest order greatly outweighs the other values to where they don’t truly matter.
2. Ignore constants
- When looking at time complexity, we are looking primarily for trends. When adding a constant to an equation, the ‘speed’ at which it trends may change, but the behavior of the shape does not. These trends are important for discovering the upper and lowers limits of whichever algorithms is being used.
- Example: the first picture has graphed f(x)=x and f(x)=3x. The second graphs f(x)=x² and f(x)=4x². While the slope of the graphs may be different in each comparative plane, the general shape of the line does not.
- In the first case, we would reduce to O(n) and the second to O(n²). n is replaceable for x in this case as both are representative of inputs.
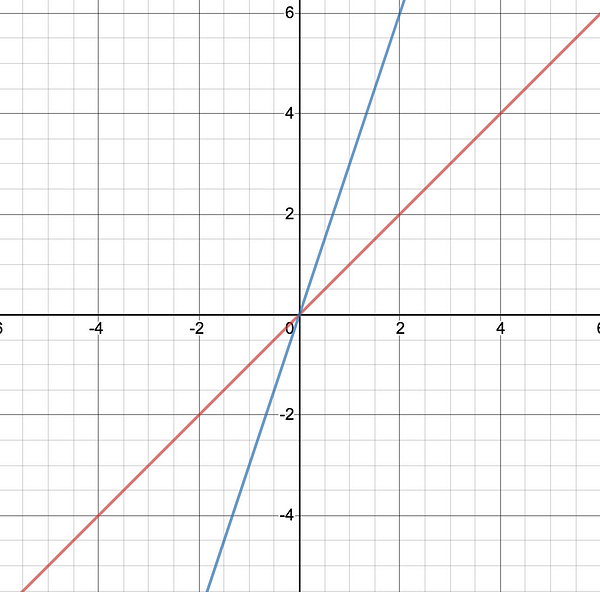
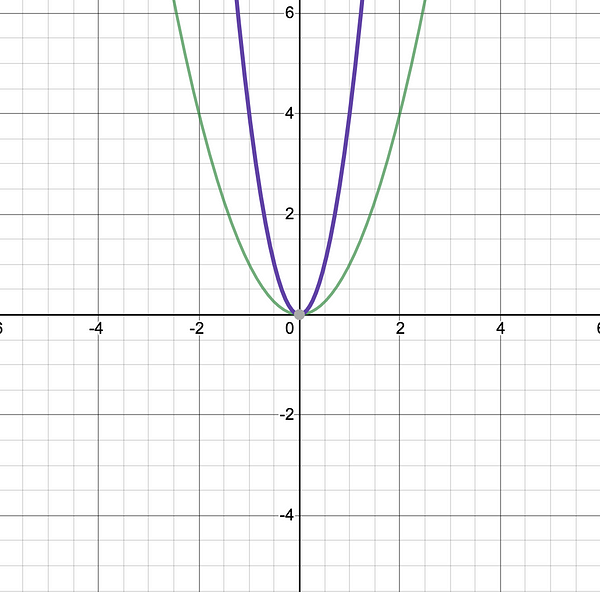
3. Consider worse case / upper bound
- “Better safe than sorry”
- When looking at time analysis, there will be times where an algorithm will take more time in certain circumstances, and less in others. In these situations, it is safer to give the higher time, worse case, for an estimate. It is better to assume the worst and have the algorithms perform better than expected, than to give a faster time, and for it to then take longer. This may not be a large issue in development, but it can cause system failure, bottlenecks, and crashes when in production.
- Example: Bubble sort, a type of sorting algorithm, has a best case of O(n) if the input is already sorted, and O(n²) if it is not sorted.
Created by: Aleia Knight
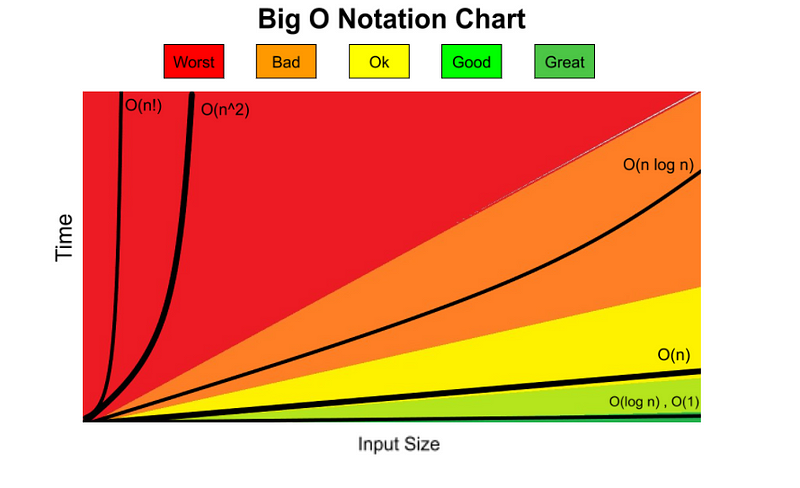
Common Big O Notations
While there are several different Big O Notations out there, alongside other notations such as Big Theta and Big Omega, the following are the most common and the most often seen.
O(1) — Constant Time
- Runs in the same time regardless of the size of the input data set.
- Common examples include reading from a file, printing to console, or inserting in a sorted array.
O(n) — Linear Time
- Runs in time directly proportional and grows linearly to the size of the input data set.
- A common example is traversing through a list.
O(n²) — Quadratic Time
- Runs in time directly proportional to the square of the size of the input data set.
- Common examples would be sorting algorithms like bubble sort or insertion sort, where the entire list must be looked through, for every element in the original list, i.e. nested loops.
O(log n) — Logarithmic Time
- Runs in time proportional to the logarithm of the input.
- The most common example is binary search, where, in each iteration, the input is halved.
Finding Best and Worst Case
As stated before, the more important number is the worse case. However, finding both is crucial for understanding range.
To find best and worst case:
- Look at the operations executed in the code (variable assignments, iterations, loops, print/returns, etc.)
- See how many times each is executed and sum them together.
- Reduce the equations using the rules stated above.
Tips/Tricks:
- Printing, returning, and variable assignments are O(1)
- Single loops are often O(n).
- Nested loops are often O(n²)
- When input is continuously getting halved, it is often O(log n).
This is just the beginning!
And, as with many things with computer science and mathematics, it only truly make sense with practice and repetition.
Interview Cake has a series of questions to practice Big O notations here → Big O Notation Practice Questions
If memorization is more your forte, here is a cheat sheet → Big O Notation Cheatsheet
Happy coding!